Даже при успешном исследовании невидимого мира средствами математики выяснение физического и геометрического смысла полученных результатов может обернуться непростой самостоятельной задачей. Так было с теорией относительности, в не меньшей мере это свойственно и квантовой механике. В 1926 году Макс Борн дал вероятностное истолкование пси-функции. Для отдельно взятой микрочастицы квадрат модуля ее пси-функции Ψ(х, у, z, t) определяет вероятность нахождения частицы в момент времени t в окрестности точки с координатами х, у, z. Можно так подобрать постоянный множитель для пси-функции частицы, чтобы вероятность нахождения этой частицы во всем бесконечном объеме наблюдаемого пространства равнялась единице, как принято для достоверного события. Тогда если практически близкая к единице вероятность нахождения частицы придется на достаточно малую область пространства, эта область может считаться приблизительно точечной и восприниматься в эксперименте как материальная точка. Но рассматривая значительно меньшие области пространства, мы будем получать для них с помощью пси-функции вероятности нахождения частицы значительно меньшие, чем единица, и уже бес c мысленно будет ставить вопрос, в какой из этих областей достоверно находится частица. Значит локализация частицы в строгом смысле становится неопределенной и бессмысленно говорить о траектории ее движения. Вместо траектории частицы мы имеем дело с полем вероятностей, характеризуемым волновой функцией, и частица может проявиться в любой точке этого поля без непрерывного перемещения через близкие к ней точки.
Таким образом, для квантовой механики материальная точка представляет не безусловную основу материальных объектов, а внешнюю форму проявления процессов, совершающихся на более глубоком и тонком уровне материальных форм, который обнаруживается за уровнем телесным, корпускулярным. Уместно назвать такой более глубокий уровень материи субкорпускулярным.
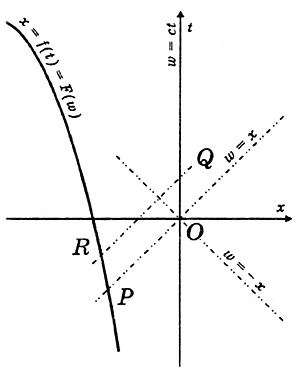
Теория относительности по-своему, с иной стороны выявляет тот факт, что материальные точки (тела) представляют внешнюю форму проявления объектов, радикально отличных от тел. Мы наблюдаем материальную точку не иначе как в определенном месте пространства, характеризуемом координатами х, у, z в определенный момент времени t. Каждое такое событие выражается совокупностью чисел (х, у, z, t). Если для простоты и наглядности ограничиться рассмотрением только одномерных движений материальной точки (вдоль оси Ох), то каждое событие будет представлено парой чисел (х, t). Тогда зависимость пространственной координаты х от времени t, выраженную функцией х=f(t), можно будет изобразить на плоскости в виде линии, называемой графиком движения материальной точки. Герман Минковский предложил модель строения мира, в которой образование, родственное графику движения, выступает в роли материального объекта, определяющего поведение тел. Минковский назвал такой объект мировой линией. Мировые линии формируются самой природой, причем в пространстве, отличном от наблюдаемого.
Минковский был первым, кто понял, что в законах теории относительности выражены геометрические отношения, присущие пространству с непривычными для нас метрическими свойствами, т.е. с иными правилами сравнения длин непараллельных отрезков и определения величин углов, чем в наблюдаемом пространстве. Например, в пространстве Минковского расстояние между двумя точками по прямой больше, чем по ломаной или кривой линии, соединяющей эти точки. В пространстве Минковского имеются специфические направления (прямые), называемые изотропными, вдоль которых метрическое расстояние между любыми различными точками равно нулю, чего не может быть в наблюдаемом пространстве. Все особенности метрических свойств пространства Минковского сконцентрированы в том факте, что операция скалярного умножения векторов определена в нем несколько иначе, чем в наблюдаемом пространстве. Для обозначения этого различия говорят, что наблюдаемое пространство обладает собственно евклидовыми, а пространство Минковского — псевдоевклидовыми метрическими свойствами.
Наблюдаемое пространство трехмерно, и его система координат строится на трех взаимно перпендикулярных осях Оx, Оy, Оz. Пространство Минковского четырехмерно: в нем в дополнение к таким же координатным осям Ох, Оу, Оz имеется четвертая ось координат Оw, перпендикулярная к каждой из трех первых. В направлении оси Оw отсчитывается координата w=ct, пропорциональная времени (коэффициент с=300000 км/сек представляет собой универсальную электродинамическую постоянную, проявляющуюся в частности в качестве скорости света). В равенстве w=ct выражена наиболее кратко, ярко и общедоступно суть открытия Минковского: то, что мы воспринимаем как течение времени t, оказывается формой проявления пространственной протяженности w. Подобную мысль высказывал еще Блаженный Августин (354—430 гг. н.э.): «Теперь я вижу, что время есть действительно какое-то протяжение... Итак, надобно полагать, что и прошедшее, и будущее время также существуют, хотя непостижимым для нас образом». («Антология мировой философии», том I, стр. 588, 587, М.: Мысль, 1969). Но это оставалось чисто умозрительным утверждением, а классической физике с ее количественно определенными и практически подтвержденными закономерностями мысль о сводимости времени к пространственной протяженности была чужда, пространство и время рассматривались как две принципиально различные формы существования материи.









